現在の最新版 Ver.1.4.5 バレルの空気抵抗や、フライトのピッチングモーメントなども入れて精度を上げました。間違いを修正しました。(2020/6/13) Google Worksheetsでできていますので、ご自分のGoogle アカウントに保存すると計算上のフライトなどのセッティングを変更することができます。
Ver1.2.3 計算が遅かったので速くしました。 ファイル→コピーを作成で、パラメーターを変更できるようになります。 (2020/4/25)
ダーツ の軌跡飛型計算 Ver1.1 の公開版となんでスタンダードフライトなのか ダーツ の軌跡飛型計算 Ver1.2 の公開版で、投げ方、セッティング、投げる環境、リリース位置によりどのようにダーツが飛んで行くかの計算を示しました。使い方については、Ver.1.1の記事をご参照ください。
Googleスプレッドシートだけで行なっていて、誰でも簡単にパラメーターを変更することができます。マクロは使っていませんので安心です。3種類の場合の計算を行なって比較できるようになっていて、それぞれの計算はワークシートの名称「1」,「2」,「3」で行っています。
どのように計算しているのか、なにが考慮に入っていて、なにを考慮していないかを示すのと、自分でなにをやったか忘れるので記録しておくために以下にパラメーターと計算式を示します。
ダーツの軸周りのスクリュー回転を考慮してフライトの面積を補正しました。ダーツ軌跡飛型計算Ver.1.2.1のダウンロードはこちらから。さらに、グラフにフライトを付け加えたました。そのVer.1.2.2のダウンロードはこちらから。数値を変えるには、Googleのアカウントが必要になります。メニューから「ファイル」「コピーを作成」英語版がでる場合には「File」「Make a copy」で自分のドライブにコピーすると行えるようになります。英語版のVer.1.2.2はこちらです。
初期高さ ダーツが手から離れる高さ。身長ではありません。
ボードまでの距離 ダーツをリリースした点からボードまでの距離。スローラインからボードまでの距離ではありません。前傾したり腕を前に出すのでスローラインからボードまでの距離よりも短くなります。
初期速度 ダーツ をリリースした時のダーツ の速さ
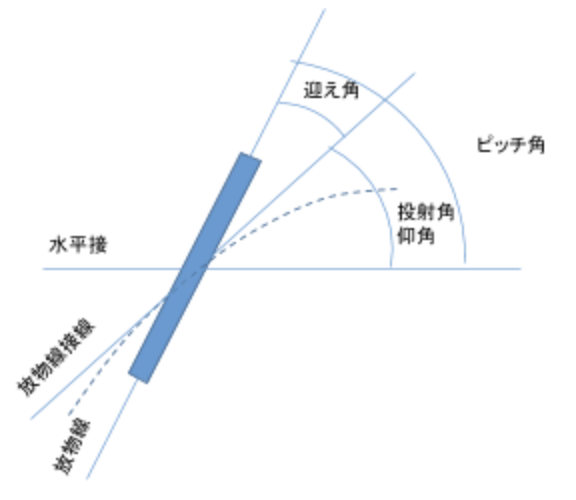
投射角 ダーツをリリースしたとき の重心の方向と水平がなす角度 ダーツ をボードに当てるには上に投げ上げることになるので正の値を持つ。
初期迎え角 β ダーツ の重心の移動方向に対してのダーツ の傾き。水平に対してではない。投射角が重心の移動方向になるのでその方向と一致していれば0°となる。
初期回転速度 ダーツ をリリースしたときに、一秒に何回転する回転速度でリリースしているかを示す。リリースした瞬間に先端が上方向に一秒に1回転するように回転していれば1となる。実際にはフライトの働きでそのまま回転はせずにまた先端が先を向くことになるが、最初にどのようにリリースしているかが重要になる。所謂裏抜きになっているか表抜きになっているかである。先端が上に向くように(裏抜きで)投げていれば正の値になり、下に向くように(表抜きで)投げていれば負の値になる。
ポイント長さ バレル先端からダーツ 先端までの距離。ポイントを抜いたときの全長ではなく露出している長さである。ダーツ の慣性モーメントとボードに最初に当たる先端の位置を決めるのに必要。
ポイント質量 ポイントの重さ。厳密には露出している部分の重さとしたいが、測定不可能なのでポイントの全重量と等しいと近似する。
バレル長さ バレル部分の長さ 実測するかメーカー公表の値を用いる。
バレル質量 バレルの重さ 実測するかメーカー公表の値を用いる。
シャフト バレルの後端からフライトの先端まで。シャフトそのものの長さではない。
シャフト スリット部長さ フライトを入れるために切り欠いている長さ。この長さとシャトの長さを足してシャフトの全長としている。ネジ部の長さは無視している。
シャフト質量 シャフトの重さ。厳密には露出している部分の重さとしたいが、測定不可能なのでシャフトの全重量と等しいと近似する。
フライト長さ フライトの先端から後端までの長さ。幅ではない。
フライト重さ フライト1枚の重さ
フライト形状 スタンダード、ティアドロップ、シェイプ、カイト、ロケット、スリム、アストラ、ブレット、Zの中から選ぶ。ない場合は近いものにする。
場所 重力が違うため緯度の近い都市名を選ぶ。
気温 投げる環境の気温。空気の密度が異なると影響があり、空気の密度は気温と気圧と湿度から計算できるため
気圧 投げる環境の気圧。空気の密度が異なると影響があり、空気の密度は気温と気圧と湿度から計算できるため
湿度 投げる環境の気圧。空気の密度が異なると影響があり、空気の密度は気温と気圧と湿度から計算できるため
軌道の計算は初期速度と投射角からの重力を受ける放物線の計算がベースになり、それに、フライトが受ける抗力による減速の影響と若揚力による落下速度の減速の影響を加えてあります。ダーツが常に重心の移動方向に向いていて 振動がない場合は、フライトに空気が当たらないので放物線になります。バレルやシャフトに空気が当たることによる抗力、揚力は計算してません。フライトだけです。
飛型の計算は迎え角と初期回転速度を初期値として、フライトが受ける抗力と揚力によるダーツ の重心を中心とした振動によるを計算しています。ダーツ の慣性モーメントと重心位置は、入力したダーツ のパーツの長さと重さから計算しています。
揚力と抗力は岡本正人,上馬義貴,「低レイノルズ数における翼の平面形空力特性の実験的研究」, 秋田高専研究紀要,Vol.44,p42-50(2008)に示されていた値を用いています。揚力と抗力は翼の形から計算で求めても実際とは合わないので、どうしてもこのような実験で求めた値が必要になります。三角翼、楕円翼、矩形翼の揚力係数、抗力係数が0°〜90°まで示されています。グラフからデータを読み取って数値化し、ワークシートのCDに抗力係数、CLに揚力係数を示しました。抗力は角度がマイナスの場合には符号を逆転した正の角度の値と同じになり、揚力は符号を逆転した正の角度の値と逆の値になると考えられます。抗力は翼の角度が風の向きに対して上を向いていても下を向いていても同じです。揚力は、風の向きに対して上を向いていれば上に上がる力となり、下を向いていれば下に下がる力が生まれ方向が逆転するからです。迎え角が90°を超えることは、実際にはほとんど起こりませんが、抗力の場合は90°を軸に対称となり、揚力の場合は90°の軸を対称としてさらに符号が逆になります。揚力の場合は、90°を超えると力の向きが上から下に反転するためです。以上のように考えて、0〜90°までのデータを0°から360°に計算時に換算しなくてよいようにあらかじめ展開しています。
計算方法について、投げた直後から、角度が変わる揚力と抗力が変わり、それにしたがって、横方向、縦方向の速度が影響を受け、ダーツ の角度が変わり、それによりまた揚力と抗力が変わるので、時間を入れれば重心の位置やダーツ の角度が得られるような方程式を立てるのは困難です。そのため、オイラー法と呼ばれている方法を用いました。ダーツ が飛んでいる時間を1000等分にして微小時間(約0.4/1000秒)に分けます。初期値から微小時間後のダーツ の位置、角度と速度を計算し、その計算値を元に次の微小時間後のダーツ の位置、角度、速度を計算していっています。この分割数が荒すぎると、実際の現象を予測できませんが、かなり細かくすれば、その微小時間内での変化が曲線的でも直線的であると近似することができるので、精度の高い近似値を計算することができます。ルンげ・クッタ法というオイラー法よりやや精度が高い方法もありますが、表計算で全て行った都合上、単純なオイラー法を用いました。重心の位置とダーツの傾きの各時間で計算するために用いた計算式は以下の通りです。
重心位置の計算
K(t)=K(t-dt)+AB(t-dt)・dt, K(0)=0
L(t)=L(t-dt)+AC(t-dt)・dt, L(0)=B4
K(t):重心の飛行距離
AB(t):時間tでの横方向の速度
L(t):時間tでの重心の高さ
B4:初期重心高さ
t:時間 dt:微小時間
AC(t):時間tでの横方向の速度
パラメーターで(t)は「時間tでの」を意味するので以下省略します。
AB(t)=AB(t-dt)+AR(t-dt)dt, AB(0)=B44
AC(t)=AC(t-dt)+AQ(t-dt)dt, AC(0)=B45
K(t):重心の飛行距離
AR(t):時間tでの横方向の加速度
L(t):時間tでの重心の高さ
B4:初期重心高さ
t:時間 dt:微小時間
AQ(t):時間tでの横方向の加速度
AR(t)={AN(t)・cos(X(t)+Z(t))}/B40
AN(t):遠心力 (ダーツの縦振動による軸方向にかかる力)
X(t):仰角
Z(t):迎え角
B40:ダーツ の全質量
AQ(t)={-AN(t)・sin(X(t)+Z(t))-B40・B68}/B40
B68:重力加速度
AN(t)=AG(t)cos(Z(t))-(ABS(AH(t))sin(Z(t))sign(cos(Z(t)))
AG(t):フライトが受ける抗力
-90°<Z(t)<90°ではcos(Z(t))は正の値となる。すなわち、抗力は遠心力になる。90°<Z(t)<270°ではcos(Z(t))は負の値となる。すなわち、抗力は負の遠心力(向心力)になる。
AG(t)=AD(t)^2・AE(t)・B51・B50/2
AD(t):重心の速度
AE(t):迎え角Z(t)でのCD値
B51:空気の密度
B51=1.293・273.15/(273.15+B24)(B25-(0.387B64)/1013.25
B24:気温
B25:気圧
B64:水蒸気圧
B64=(B24^2・B65+B24・B66・B67)B26/100
B26:湿度
B65:飽和水蒸気圧近似式二次の項
B66:飽和水蒸気圧近似式一次の項
B67:飽和水蒸気圧近似式定数項
B50:代表面積
B50=S・2/(pi/2)
S:最大投影面積
最大投影面積を直角に同じ翼があるため2倍し軸の周りに平均化するため(pi/2)で割る。(ver.1.2.1より) 直行した羽のない2枚羽なら回転していたら投影面積は正弦波に比例して変化するはず。0から360°(2π)までを正弦波の絶対値で積分すると4となる。一方、矩形波の場合は2π。そのため回転すると断面積は2/piとなる。
AH(t):フライトが受ける揚力
遠心力が重心から外向きの場合が正、内向きを負とすると、以下のような関係になるので揚力の絶対値にsin(Z(t))を掛けて軸方向の力に変換した後、cos(Z(t))の符号を掛け、全体の符号はマイナスとした。
0°<Z(t)< 90° 揚力>0 揚力の遠心力成分<0, sin>0, cos>0
90°<Z(t)<180° 揚力<0 揚力の遠心力成分>0, sin>0, cos<0
180°<Z(t)<270° 揚力>0A揚力の遠心力成分>0, sin<0, cos<0
270°<Z(t)<360° 揚力<0 揚力の遠心力成分<0, sin<0, cos>0
AH(t)=AD(t)^2・AF(t)・B51・B50/2
AD(t):重心の速度
AF(t):迎え角Z(t)でのCL値
B51:空気の密度
空気抵抗応力
1/2 (空力中心距離*角速度)^2*代表面積*90°のときのCD値)
ダーツの傾き
ダーツの水平に対する傾きは仰角Y(t)と迎え角AA(t)の和なのでそれぞれ計算する。
Y(t)=atan(AC(t)/AB(t))
AA(t)=AA(t-dt)+AS(t-dt)dt, AA(0)=B47
B47:初期迎え角
AS(t):角速度
AS(t)=AS(t-dt)+AU(t)dt, AS(0)=B39
AU(t):角加速度
B39:初期角速度(初期回転速度)
AU(t)=AK(t)・B48/B56
AK(t):回転方向の応力と抗力の合わせた力
AK(t)=AI(t)+AJ(t)
AI(t):フライトの抗力と揚力により生じる回転方向応力
AI(t)=[abs{AG(t)sin(Z(t))}+abs{AH(t)cos(Z(t))}]・sign(-sin(z2)) 揚力・抗力の回転方向成分は同方向で0°〜180°では負(反時計周り)、180°〜360°では正(時計回り)となる。
AJ(t):回転することにより生じるフライトに垂直な空気抵抗応力
AJ(t)={B48・AS(t)}^2・B50・B51/2
B48:重心から空力中心までの距離
B48=(B12+B14-B57)+B16+B19/4
どのフライトでもフライトの前から1/4のところに空力中心があると仮定する
B12:ポイント長さ
B14:バレル長さ
B16:バレル-フライト間長さ
B19:フライト長さ
B57:重心からダーツ先端までの長さ
B57=((B20+B18+B13)/B36+B14)/2+B12-(B13/B36)
B18:シャフト重さ
B20:フライト重さ
B36:バレル密度
B13:ポイント重さ
B14バレル長さ
B56:慣性モーメント
B56=B52+B53+B54+B55
B52:ポイントの慣性モーメント
B52=B35/3*(B57^3-(B57-B12)^3)
B35:ポイントの単位長さあたりの重さ (ポイント重さ/ポイント長さ)
B53:バレルの慣性モーメント
B53=B36/3*(B61^3-(-B62)^3)
B36:バレルの単位長さあたりの重さ (バレル重さ/バレル長さ)
B61:重心からバレル先端までの長さ B57-B12
B62:重心からバレル末端までの長さ (B12+B14)-B57
B54:シャフトの慣性モーメント
B54=B37/3・(B60^3-B62^3)
B37:シャフトの単位長さあたり重さ (シャフト重さ/シャフト長さ)
B60:重心からシャフト末端までの距離
B62:重心からバレル末端までの距離
B55:フライトの慣性モーメント
B55=B38/3・(B58^3-B59^3)
B38:フライトの単位長さあたりの重さ(フライトの重さ/フライトの長さ)
B58:重心からダーツ後端までの距離
B59:重心からフライト先端までの距離
[…] 【最新版】数式の微修正とフライトの軸周りの回転を考慮しました。ダーツの軌跡飛型計算Ver.1.2.1 (2018/9/16) […]
[…] 【最新版】数式の微修正とフライトの軸周りの回転を考慮しました。ダーツの軌跡飛型計算Ver.1.2.1 (2018/9/16) […]
[…] ダーツの飛び方の計算を行った結果では、シャフトの長さが変わって変わるのはダーツの重心の軌道ではなく、ダーツの縦方向の振動の速さでした。物は放物線を描いて飛びますので、 […]